Boolean_Functions
This example shows the proper handling of the class SCIL::boolfunction.We first create a new instance IP of an SCIL::ILP_Problem. (In this example it is a maximization problem)
ILP_Problem IP(Optsense_Max);
var x0 = IP.add_binary_variable(0.); var x1 = IP.add_binary_variable(2.); var x2 = IP.add_binary_variable(0.); var x3 = IP.add_binary_variable(0.); var x4 = IP.add_binary_variable(1.);
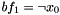 . The last parameter is true, if the created boolean function should be negated.
. The last parameter is true, if the created boolean function should be negated. boolfunction* bf1 = new boolfunction(x0, true);
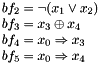
boolfunction* bf2 = new boolfunction(x1, x2, OR, true); boolfunction* bf3 = new boolfunction(x3, x4, XOR); boolfunction* bf4 = new boolfunction(x0, x3, IMP); boolfunction* bf5 = new boolfunction(x0, x4, IMP);
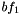 is set to
is set to 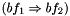 and
and 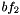 is set to
is set to 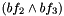 . Because
. Because 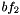 is changed after adding it to
is changed after adding it to 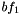 this change has no effect on
this change has no effect on 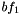 .
. bf1->add(IMP, bf2); bf2->add(AND, bf3);
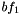 and
and 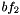 to the objective function of IP.
to the objective function of IP. IP.add_boolfunction(bf1, 1.); IP.add_boolfunction(bf2, 10.);
C1 which means that every boolean function in the given list must be true for every feasible solution. list<boolfunction*> cl; cl.push_back(bf4); cl.push_back(bf5); IP.add_bool_constraint(cl, C1);
optimize. IP.optimize();
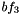 .
. delete bf3;
 1.6.3
1.6.3