Perfect_B_Matching

This example shows how to compute a perfect B matching of a given graph G using the symbolic constraint SCIL::MATCHING.

We first create an empty graph and initialize it using either the function readgraph or readgraphFromTSPLIB whichs reads a TSPLIB instance.

   Graph G;
   map<vertex_descriptor, int> node_mapG;
   map<edge_descriptor, double> edge_mapG;
   map<vertex_descriptor, int> nc;
   //if( !readgraph(base, argv[1], G, nc) )
   if( !readgraphFromTSPLIB(writeout, base, argv[filearg], G, nc, node_mapG,

We then create a new instance IP of an SCIL::ILP_Problem as a minimization problem.

   ILP_Problem IP(Optsense_Min);

The var_map VM is used to store the variables that are added to the model. These variables are binary and correspond to the edges of the graph G.

   edge_descriptor e;
   var_map<edge_descriptor> VM;
   BGL_FORALL_EDGES(e, G, Graph) {
      vl.push_back(IP.add_binary_variable(edge_mapG[e]));
      VM[e] = vl.back();
   }

map<vertex_descriptor, int> nc is used to store for each node the number of adjacent edges in the matching. The edges corresponding to variables with value 1 in an optimal solution should form a valid matching in G. To achieve this we add the symbolic constraint SCIL::MATCHING to the model.

   IP.add_sym_constraint(new MATCHING<Graph>(G, nc, VM));

As this is the only constraint, our model is now complete and we can compute an optimum solution by calling optimize.

   IP.optimize();

The optimal solution can be accessed directedly using SCIL::ILP_Problem::get_solution(). This function returns an instance of the class SCIL::solution. To obtain the objective value of the optimal solution we compute $c^Tx^*$

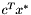for the optimal solution $x^*$

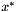stored in sol.

   //output the solution
   solution sol =  IP.get_solution();
   double sum = 0.;
   cout << "\nName: " << argv[1] << endl;
   BGL_FORALL_EDGES(e, G, Graph) {
      sum += double(edge_mapG[e]) * sol.value(VM[e]);
      if( sol.value(VM[e]) > .9 ) {
         cout << node_mapG[source(e, G)] + base << " -- ";
         cout << node_mapG[target(e, G)] + base << endl;
      }
   }
   cout << endl;
   cout.precision(2);
   cout << fixed << "solution value: " << sum << endl;