Quadratic_Assignment_Problem

This example shows how to compute a quadratic assignment using polynomials.

The format of the problem data is

n
A
B

where n is the size of the instance, and A and B are either flow or distance matrix. This corresponds to a QAP of the form 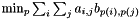where p is a permutation

First we read the coefficients and save them in matrix1 and matrix2. We then create a new instance IP of an SCIL::ILP_Problem as a minimization problem.

   ILP_Problem IP(Optsense_Min);

After this, the objective function is created by adding the necessary polynomials.

                     IP.add_polynomial(variablen[i][j]*variablen[k][l]*(matrix1[i][k]*matrix2[j][l]));

To complete our model we add the essential constraints to IP.

   //add basic constraints necessary for QAP
   row r;
   for(int i=0; i<size; i++) {
      r=0;
      for(int j=0; j<size; j++) {
         r+=variablen[i][j];
      }
      IP.add_basic_constraint(r==1,Static);
   }
   for(int i=0; i<size; i++) {
      r=0;
      for(int j=0; j<size; j++) {
         r+=variablen[j][i];
      }
      IP.add_basic_constraint(r==1,Static);
   };

Our model is now complete and we can compute an optimum solution by calling optimize.

   IP.optimize();

Finally we output the solution.

   //print solution
   for(int i=0; i<size; i++) {
      for(int j=0; j<size; j++) {
         cout<<IP.get_solution(variablen[i][j]);
      }
      cout << endl;
   };