Motivation
Motivation
Many combinatorial optimization problems are naturally formulated through constraints. Consider the traveling salesman problem TSP. It asks for the minimum cost Hamiltonian cycle in an undirected graph G = (V,E) with edge weights 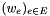 . Formulated as an optimization task:
. Formulated as an optimization task:
Find a subset T of the edges of G such that " \p T is a
Hamiltonian cycle" and 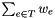 is minimum.
is minimum.
Our vision is that the sentence above (written in some suitable language) suffices to obtain an efficient algorithm for the TSP. Efficiency is meant in a double sense. We want short development time (= efficient use of human resources) and runtime efficiency (= efficient use of computer resources). The software system SCIL is our first step towards realizing this vision. Section ComputeTour shows a SCIL program for the traveling salesman problem. We propose a programming system for (mixed) integer linear programming (ILP) based on a branch-and-cut-and-price framework~(BCP) that features symbolic constraints.
Integer linear programming and more specifically the branch-and-cut-and-price paradigm for solving ILPs is one of the most effective approaches to find exact or provably good solutions of hard combinatorial optimization problems(NW88) (EGJR01). It has been used for a wide range of problems including the TSP (ABCC99) (Nad02), maximum-cut-problems (DeSimone-Rinaldi), cutting-stock-problems (VBJN93), or crew-scheduling (BJN+98). For more applications we refer to the overview (CF97). The implementation of a BCP algorithm requires significant expert knowledge, a fact that has hindered the spread of the method outside the scientific world. It consists of various involved components, each with wide influence on the algorithm's overall performance. Almost all parts of a BCP algorithm considerably rely on linear programming (LP) methods or properties of the linear programming relaxation of the underlying ILP. Many components are problem independent and can be provided by existing software packages (see (JT00)). But there is still a major problem dependent part: an ILP formulation has to be found, appropriate linear programs have to be derived, the various methods for exploiting LP solutions to find feasible solutions or speedup the computation have to be designed and implemented. To our knowledge there is no BCP system for combinatorial optimization that covers the problem dependent part in an appropriate way.
SCIL closes this gap by introducing symbolic constraints , one of the key achievements constraint programming (Hentenryck-Saraswat) into integer linear programming. It simplifies the implementation of BCP-algorithms by supporting high-level specifications of combinatorial optimization problems with linear objective functions. It provides a library of symbolic constraints, which allow one to convert high-level specifications into efficient BCP-algorithms. A user may extend SCIL by defining new symbolic constraints or by changing the standard behavior of the algorithms. We have used SCIL already in several projects like curve reconstruction (AM01) and computing protein dockings (ALKM).
Goals
We collect and motivate the goals that guided the development of SCIL. We distinguish between primary goals determining the overall design and secondary goals determining specific implementation issues.
Primary Goals
Integer linear programs frequently involve a large number of constraints and/or variables. This is either intrinsic in the problem (there are an exponential number of cut constraints in the natural formulation of the traveling salesman problem) or is algorithmically motivated (in order to use column generation, one introduces variables for high level constructs such as cycles in graphs). In either case, the set of constraints and/or variables has considerable structure and is not just an indexed collection 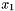 ,
, 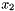 , ...,
, ..., 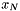 of variables for some large
of variables for some large 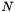 . Rather, the variables and/or constraints correspond to objects in the problem domain. We have a variable for each edge or cycle in a graph or we have a constraint for each cut in a graph. This leads to.
. Rather, the variables and/or constraints correspond to objects in the problem domain. We have a variable for each edge or cycle in a graph or we have a constraint for each cut in a graph. This leads to.
- It must be possible to refer to variables and constraints through objects in the problem domain, e.g., we should be able to talk about the variable
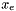 , where
, where 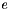 is an edge of a graph.
is an edge of a graph.
Being able to refer to single variables and constraints in a problem-oriented way, is a first step. We also want to refer to groups of variables and/or constraints. For example, we want to talk about degree constraints or cut constraints. We want to specify these constraints once and for all for an abstract graph; it should then be able to instantiate them for a concrete graph. Thus our groups of variables and/or constraints are abstract or symbolic groups. This leads to.
- It must be possible to specify structured groups of variables and/or constraints. The specification is abstract (symbolic) and can be instantiated for concrete situations.
We give an example. The cut constraints with demand 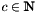 for a graph
for a graph 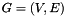 with edge variables
with edge variables 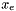 state that
state that 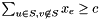 for every non-trivial cut
for every non-trivial cut 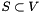 with
with 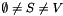 . This is a symbolic constraint which we can define once and for all and give a name, e.g.,
. This is a symbolic constraint which we can define once and for all and give a name, e.g., cut_constraints. We can then instantiate it for a concrete graph 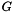 whose edges have ILP-variables associated with them through a map
whose edges have ILP-variables associated with them through a map EV and for a concrete demand, say 2, by writing cut_constraints(G,EV,2).
- Frequently used symbolic constraints are predefined and available in a library. Additional symbolic constraints can be added freely.
We have already seen in the introduction that symbolic constraints together with the ability of referring to ILP-variables through objects from the problem domain leads to concise and readable models. There is another advantage: semantic knowledge about the variables and constraints is retained and can be exploited algorithmically in the underlying branch-and-cut-and-price system.
Every node of a branch-and-cut-and-price tree has an linear program associated with it. This linear program is obtained from the complete specification by selecting some of the constraints and some of the variables. For example, only some of the cut constraints could be present and only a subset of the variables could be active. Assume that a solution to the current LP has been determined.
- Symbolic constraints can check whether they are satisfied by the current solution. If not, they can produce violated inequalities (separation) and/or promising variables (pricing). For the symbolic constraints in the constraint library these abilities are built-in. For user-defined constraints these abilities can be programmed.
Our goals have an interesting architectural consequence. When a symbolic constraint is specified and implemented, the context of its use is not known. In particular, a symbolic constraint must work without knowledge of the other variables and constraints in the model.
In different contexts different searching strategies are preferable. There are different rather general approaches and problem specific strategies.
- The user has control over the optimization process, i.e. he can choose arbitrary branching rules, he can choose an arbitrary subproblem to continue, etc. Furthermore he must be able to select from some standard strategies. An more expert user should also have the possibility to provide own methods in a library.
Secondary Goals
The first wish in this section is valid for any software project.
- Built upon existing systems as much as possible.
When we started the work on SCIL, we had experience in developing BCP-algorithms using ABACUS, LEDA, and the LP-solvers CPLEX and SoPlex. It was therefore natural to reuse these systems and to build upon the experience gained with them. The desire to reuse ABACUS and LEDA which are both implemented in C++ suggested to use C++ as the programming language for SCIL. This choice is coherent with the following goal.
- Use a programming language which is appropriate for all levels of SCIL: (1) the implementation of separation and pricing routines, (2) the implementation of search and branching strategies, (3) the language level of symbolic constraints, and (4) the specification of ILP-models.
We knew from our experience with ABACUS and LEDA that C++ supports the first two points, ILOG-solver proves that C++ is adequate for (3), and (4) follows from (3) and the ability to iterate over structures in the problem domain.
In the newest version of SCIL we have replaced LEDA with the free BOOST C++ Libraries. Thus SCIL may be used without any commercial libraries.
A general branch-&-cut algorithm has many parameters, i.e. the work on a node of a tree should could be terminated and a branching step performed, if the bound does only slightly increase during a number of iteration. Such behavior is usually controlled by parameters. The running time of such an algorithm strongly depends on the "right" selection of the parameters, but these parameters could often only be determined experimentally. Thus we want a possibility to experiment with different parameter settings without recompiling the program.
- There is a parameter file, which controls the optimization process. The parameters are also accessible in the user-defined parts.
 1.6.3
1.6.3