symmetric_connectivity

The problem is defined as follows: Given a set of nodes 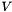$V$ and symmetric power requirements 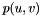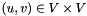$p(u,v)$ , $(u,v)\in V\times V$ , find a power assignment 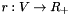$r:V \rightarrow R_+$ minimizing 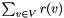$\sum_{v \in V} r(v)$ subject to the constraint that the graph 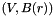$(V,B(r))$ is connected.

First, we compute the cost of the minimum spanning tree heuristic. Than, we set-up the integer programm. We have a variable for every edge of the tree supposed to be the incidencevector of the spanning tree we compute (stored in VM) and edges for the radius of a node.

double ComputeBroadcast(Graph& G, std::list<edge_descriptor>& T) {

  property_map<Graph, edge_weight_t>::type 
    cost = get(edge_weight, G);

  std::vector<edge_descriptor> MST;
  kruskal_minimum_spanning_tree(G, std::back_inserter(MST));

  std::vector<double> MSTC(num_vertices(G));
  edge_descriptor e;
  BOOST_FOREACH(e,MST) {
    MSTC[source(e,G)]=std::max(MSTC[source(e,G)], cost[e]); 
    MSTC[target(e,G)]=std::max(MSTC[target(e,G)], cost[e]);
  };

  double mstc=0;
  BGL_FORALL_VERTICES(u,G,Graph)
    mstc+=MSTC[u]*MSTC[u];

  if(0) {
    cout<<"cost of mst: " << mstc << endl;
    BOOST_FOREACH(e,MST) {
      cout << MSTC[source(e,G)] << " " << MSTC[target(e,G)] << endl;
    }
    exit(0);
  }

  ILP_Problem IP(Optsense_Min);

  var_map<edge_descriptor> VM;
  var_map<edge_descriptor> VMy;
  var_map<edge_descriptor> VMz;

  BGL_FORALL_EDGES(e,G,Graph) {
    VM[e]=IP.add_binary_variable(-0.1);
    VMy[e]=IP.add_binary_variable(cost[e]*cost[e]);    
    VMz[e]=IP.add_binary_variable(cost[e]*cost[e]);
  }


  BGL_FORALL_EDGES(e,G,Graph) {
    row r1;
    BGL_FORALL_OUTEDGES(source(e,G),f,G,Graph) if(cost[f]>=cost[e]-0.001) r1+=VMy[f];
    BGL_FORALL_INEDGES (source(e,G),f,G,Graph) if(cost[f]>=cost[e]-0.001) r1+=VMz[f];
    IP.add_basic_constraint(r1 >= VM[e]);

    row r2;
    BGL_FORALL_OUTEDGES(target(e,G),f,G,Graph) if(cost[f]>=cost[e]-0.001) r2+=VMy[f];
    BGL_FORALL_INEDGES( target(e,G),f,G,Graph) if(cost[f]>=cost[e]-0.001) r2+=VMz[f];
    IP.add_basic_constraint(r2 >= VM[e]);
  }    

  BGL_FORALL_VERTICES(u,G,Graph) {
    row r;
    BGL_FORALL_OUTEDGES(u,e,G,Graph) r+=VMy[e];
    BGL_FORALL_INEDGES( u,e,G,Graph) r+=VMz[e];
    IP.add_basic_constraint(r==1);
  };

  IP.add_sym_constraint(new SpanTree<Graph>(G,VM));


  IP.optimize();
  
  double optc=0;
  BGL_FORALL_EDGES(e,G,Graph) {
    if(IP.get_solution(VM[e])>0.5) { 
      T.push_back(e);
    };
  }
  BGL_FORALL_VERTICES(u,G,Graph) 
    MSTC[u]=0;

  BOOST_FOREACH(e,T) {
    MSTC[source(e,G)]=std::max(MSTC[source(e,G)], cost[e]);     // use updated costs from Graph G ?
    MSTC[target(e,G)]=std::max(MSTC[target(e,G)], cost[e]);
  };
  BGL_FORALL_VERTICES(u,G,Graph)
    optc+=MSTC[u]*MSTC[u];

  cout<<"Number of nodes "<<num_vertices(G)<<endl;
  cout<<"Cost of mst "<<mstc<<"\n";
  cout<<"Cost of optimal solution "<<optc<<"\n";

  cout<<"Save "<<(mstc-optc)/mstc*100<<"\n";


  return (mstc-optc)/mstc*100;
} // END_COMPUTE_BROADCAST