ABA_SORTER< ItemType, KeyType > Class Template Reference

This class implements several functions for sorting arrays according to increasing keys. More...

#include <sorter.h>

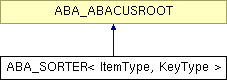
Inheritance diagram for ABA_SORTER< ItemType, KeyType >:

ABA_ABACUSROOT List of all members.

Public Member Functions

 ABA_SORTER (ABA_GLOBAL *glob)
void quickSort (int n, ABA_ARRAY< ItemType > &items, ABA_ARRAY< KeyType > &keys)
 Sorts the elements of an array of n items according to their keys.
void quickSort (ABA_ARRAY< ItemType > &items, ABA_ARRAY< KeyType > &keys, int left, int right)
void heapSort (int n, ABA_ARRAY< ItemType > &items, ABA_ARRAY< KeyType > &keys)

Private Member Functions

int partition (ABA_ARRAY< ItemType > &items, ABA_ARRAY< KeyType > &keys, int left, int right)
 Returns a number q ({{left <= q <= right)} and guarantees that all elements i with {key[i] <= key[q]}} are stored in the left part of the array, i.e., in items[left], , items[q], and all elements j with key[j] > key[q] are stored in the right part of the array, i.e., in items[q+1], $\dots$, items[right].
void buildHeap (int n, ABA_ARRAY< ItemType > &items, ABA_ARRAY< KeyType > &keys)
 Resorts the elements if items and keys such that the heap property holds, i.e., keys[i] >= keys[2*i+1] and keys[i] >= keys[2*i+2].
void heapify (int n, ABA_ARRAY< ItemType > &items, ABA_ARRAY< KeyType > &keys, int root)
 Assumes that the heap property holds for the subtrees rooted at the sons of root and restores the heap property for the subtree rooted at root.
void check (int n, ABA_ARRAY< ItemType > &items, ABA_ARRAY< KeyType > &keys)
 Is a debugging function and terminates the program with an error message if the elements of items are not sorted by increasing keys.

Private Attributes

ABA_GLOBAL * glob_
ItemType itemSwap_
KeyType keySwap_

Detailed Description

template<class ItemType, class KeyType>
class ABA_SORTER< ItemType, KeyType >

This class implements several functions for sorting arrays according to increasing keys.

Definition at line 46 of file sorter.h.

Constructor & Destructor Documentation

template<class ItemType, class KeyType>
ABA_SORTER< ItemType, KeyType >::ABA_SORTER ( ABA_GLOBAL *  glob  ) 

The constructor.

Parameters:
glob A pointer to the corresponding global object.

Member Function Documentation

template<class ItemType, class KeyType>
void ABA_SORTER< ItemType, KeyType >::quickSort ( int  n,
ABA_ARRAY< ItemType > &  items,
ABA_ARRAY< KeyType > &  keys 
)

Sorts the elements of an array of n items according to their keys.

This function is very efficient for many practical applications. Yet, has a worst case running time of 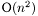$\hbox{\rm O}(n^2)$.

Parameters:
n The number of elements being sorted.
items The items being sorted.
keys The keys of the sorted items.

template<class ItemType, class KeyType>
void ABA_SORTER< ItemType, KeyType >::quickSort ( ABA_ARRAY< ItemType > &  items,
ABA_ARRAY< KeyType > &  keys,
int  left,
int  right 
)

Sorts an partial array.

The function quickSort() uses the divide-and-conquer technique. First the function partition() puts the small elements to the left part and all big elements to the right part of the array being sorted. More precisely, it holds then, keys[i] <= keys[q] for all i in left, q and keys[q] < keys[i] for all i in q+1, right. Hence, it is sufficient to sort these two subarrays recursively.

Parameters:
items The items being sorted.
keys The keys of the items.
left The first item in the partial array being sorted.
right The last item in the partial array being sorted.

template<class ItemType, class KeyType>
void ABA_SORTER< ItemType, KeyType >::heapSort ( int  n,
ABA_ARRAY< ItemType > &  items,
ABA_ARRAY< KeyType > &  keys 
)

Sorts an array of n items according to their keys.

In many practical applications this function is inferior to quickSort(), although it has the optimal worst case running time of 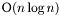$\hbox{\rm O}(n\log n)$.

The function heapSort() generates a heap. This guarantees that the largest element is stored in items[0]. So it is obvious that if we want to sort the items by increasing keys, this element will finally be stored in items[n-1]. Hence we swap the items and keys of 0 and n-1 and restore the heap property for the elements 0,, n-2. This can be done by heapify() since the subtree rooted at 1 and 2 are still heaps (the last element is not considered anymore). This process is iterated until the elements are sorted.
Parameters:
n The number of items being sorted.
items The items being sorted.
keys The keys of the items.

template<class ItemType, class KeyType>
int ABA_SORTER< ItemType, KeyType >::partition ( ABA_ARRAY< ItemType > &  items,
ABA_ARRAY< KeyType > &  keys,
int  left,
int  right 
) [private]

Returns a number q ({{left <= q <= right)} and guarantees that all elements i with {key[i] <= key[q]}} are stored in the left part of the array, i.e., in items[left], , items[q], and all elements j with key[j] > key[q] are stored in the right part of the array, i.e., in items[q+1], $\dots$, items[right].

Parameters:
items The items being sorted.
keys The keys for sorting the items.
left The left border of the partial array being considered.
right The right border ot the partial array being considered.
First, we determine a pivot element k. The while loop stops by returning r as soon as the elements are partitioned in two subsets such all elements i in left <= i <= r have a smaller key than the elements i with r+1 <= right.
The do-loops stop as soon as a pair of elements is found violating the partition property. This pair of elements is the swapped together with their keys.

template<class ItemType, class KeyType>
void ABA_SORTER< ItemType, KeyType >::buildHeap ( int  n,
ABA_ARRAY< ItemType > &  items,
ABA_ARRAY< KeyType > &  keys 
) [private]

Resorts the elements if items and keys such that the heap property holds, i.e., keys[i] >= keys[2*i+1] and keys[i] >= keys[2*i+2].

Parameters:
n The number of elements of the following arrays.
items The items being sorted.
keys The keys for sorting the items.
The function heapify() is called for each node of the tree which is not necessarily a leaf. First nodes on higher level in the tree processed.

template<class ItemType, class KeyType>
void ABA_SORTER< ItemType, KeyType >::heapify ( int  n,
ABA_ARRAY< ItemType > &  items,
ABA_ARRAY< KeyType > &  keys,
int  root 
) [private]

Assumes that the heap property holds for the subtrees rooted at the sons of root and restores the heap property for the subtree rooted at root.

Parameters:
n The number of elements of the following arrays.
items The items being sorted.
keys The keys for sorting the items.
root The index where the heaps property has to be restored.
The function heapify() checks if the heap property holds for root. This is not the case if the largest element of l, r, and root is not root. In this case the elements of root and largest are swapped and we iterate. Otherwise, the heap property is restored.

template<class ItemType, class KeyType>
void ABA_SORTER< ItemType, KeyType >::check ( int  n,
ABA_ARRAY< ItemType > &  items,
ABA_ARRAY< KeyType > &  keys 
) [private]

Is a debugging function and terminates the program with an error message if the elements of items are not sorted by increasing keys.

Parameters:
n The number of elements of the following arrays.
items The items being sorted.
keys The keys for sorting the items.

Member Data Documentation

template<class ItemType, class KeyType>
ABA_GLOBAL* ABA_SORTER< ItemType, KeyType >::glob_ [private]

A pointer to the corresponding global object.

Definition at line 183 of file sorter.h.

template<class ItemType, class KeyType>
ItemType ABA_SORTER< ItemType, KeyType >::itemSwap_ [private]

An auxiliary variable for swapping items.

Definition at line 187 of file sorter.h.

template<class ItemType, class KeyType>
KeyType ABA_SORTER< ItemType, KeyType >::keySwap_ [private]

An auxiliary variable for swapping keys.

Definition at line 191 of file sorter.h.

The documentation for this class was generated from the following file:
Generated on Tue Aug 14 18:09:59 2007 for ABACUS by  doxygen 1.5.1