SCIL::ATOUR< Graph > Class Template Reference

The symbolic constraint for directed Hamiltonian cycles. More...

#include <atour.h>

Inheritance diagram for SCIL::ATOUR< Graph >:

[legend]

Collaboration diagram for SCIL::ATOUR< Graph >:

[legend]

List of all members.

Classes
class	dir_cutset_inequality
class	dir_cutset_inequality
class	dir_degree_equality
class	dir_degree_equality
Public Member Functions
	ATOUR (Graph &G_, var_map< edge_descriptor > &X)
	Constructor.
void	init (subproblem &S)
status	standard_separation (subproblem &S)
status	fast_separation (subproblem &S)
status	feasible (solution &S)
void	info ()

Detailed Description

template<typename Graph>
class SCIL::ATOUR< Graph >

This symbolic constraints takes as arguments a directed graph G and a var_map<edge> X. X has to map every edge of the graph to a binary variable.

The feasible assignments of the symbolic constraint are those where the vector of the variables associated with the edges of the graph is an incidence-vector of a directed Hamiltonian cycle.

The symbolic constraint uses the cutting plane method, based on the well known subtour elimination formulation of directed Hamiltonian cycles.

Definition at line 33 of file atour.h.

Constructor & Destructor Documentation

template<typename Graph >

ATOUR::ATOUR	(	Graph &	G_,
		var_map< edge_descriptor > &	X
	)			`[inline]`

Ensures that the edges in X form a Hamiltonian cycle.

Preconditions:

The variables associated to the edges are binary.

Parameters:

ATOUR_Debug_Out true|false

Definition at line 92 of file atour.h.

Member Function Documentation

template<typename Graph >

ATOUR< Graph >::status ATOUR::fast_separation ( subproblem & S ) [inline, virtual]

Separates the subtour elimination constraints, i.e. 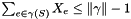$\sum_{e \in \gamma(S)} X_e \le \| \gamma \| -1$ for all 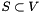$S \subset V$ , only with a heuristic.

Reimplemented from SCIL::sym_constraint.

Definition at line 239 of file atour.h.

template<typename Graph >

ATOUR< Graph >::status ATOUR::feasible ( solution & S ) [inline, virtual]

Returns true, if the induced graph is connected.

Reimplemented from SCIL::sym_constraint.

Definition at line 260 of file atour.h.

template<typename Graph >

void ATOUR::info ( ) [inline, virtual]

Returns information on the symbolic constraints.

Reimplemented from SCIL::sym_constraint.

Definition at line 280 of file atour.h.

template<typename Graph >

void ATOUR::init ( subproblem & S ) [inline, virtual]

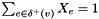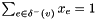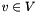Adds the degree constraints, i.e. $\sum_{e \in \delta^+(v)} X_e = 1$ and $\sum_{e \in \delta^-(v)} x_e = 1$ for all $v \in V$ , to the LP.

Reimplemented from SCIL::sym_constraint.

Definition at line 108 of file atour.h.

template<typename Graph >

ATOUR< Graph >::status ATOUR::standard_separation ( subproblem & S ) [inline, virtual]

Separates the subtour elimination constraints, i.e. 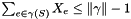$\sum_{e \in \gamma(S)} X_e \le \| \gamma \| -1$ for all 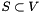$S \subset V$ , with a heuristic and an exact separation algorithm.

Reimplemented from SCIL::sym_constraint.

Definition at line 247 of file atour.h.

The documentation for this class was generated from the following files:

SCIL::ATOUR< Graph > Class Template Reference

Classes

Public Member Functions

Detailed Description

template<typename Graph> class SCIL::ATOUR< Graph >

Constructor & Destructor Documentation

Member Function Documentation

template<typename Graph>
class SCIL::ATOUR< Graph >