Main Page Class Hierarchy Compound List File List Contact Download Symbolic Constraints Examples

SCIL::PATH

SCIL::PATH< Graph > Class Template Reference

The symbolic constraint for supersets of path. More...

#include <path.h>

Inheritance diagram for SCIL::PATH< Graph >:

Inheritance graph

Collaboration diagram for SCIL::PATH< Graph >:

Collaboration graph

List of all members.

Classes
class	path_cutset_inequality
Public Member Functions
	PATH (Graph &G, vertex u, vertex v, var_map< edge_descriptor > &X)
status	standard_separation (subproblem &S)
status	feasible (solution &S)
void	info ()

Detailed Description

template<typename Graph>
class SCIL::PATH< Graph >

This symbolic constraints takes as agruments a directed graph G, a source node u, a target node v and a var_map<edge> X. X has to map every edge of the graph to a binary variable.

The feasible assignments of the symbolic constraint are those where the vector of the variables associated with the edges of the graph is an incidencevector of a subgraph of G where there is a path from u to v.

The symbolic constraint uses the cutting plane method.

Examples:: Diameter_Constraint_Minimum_Spanning_Tree.

Definition at line 33 of file path.h.

Constructor & Destructor Documentation

template<typename Graph >

PATH::PATH	(	Graph &	G,
		vertex	u,
		vertex	v,
		var_map< edge_descriptor > &	X
	)			`[inline]`

Ensures that the edges in X form a superset of a path from u to v.

Preconditions:

The variables associated to the edges are binary. Parameters:
PATH_Debug_Out true|false

For a demo, see: ptsp.c .

Definition at line 52 of file path.cc.

Member Function Documentation

template<typename Graph >

PATH< Graph >::status PATH::feasible ( solution & S ) [inline, virtual]

Tests if there is a path from u to v.

Reimplemented from SCIL::sym_constraint.

Definition at line 163 of file path.cc.

References SCIL::subproblem::configuration(), and SCIL::solution::value().

template<typename Graph >

void PATH::info ( ) [inline, virtual]

Returns information on the symbolic constraints.

Reimplemented from SCIL::sym_constraint.

Definition at line 186 of file path.cc.

template<typename Graph >

PATH< Graph >::status PATH::standard_separation ( subproblem & S ) [inline, virtual]

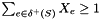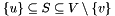Separates the constraints $\sum_{e \in \delta^+(S)} X_e \ge 1$ for all $\{ u \} \subseteq S \subseteq V \setminus \{ v \}$ .

Reimplemented from SCIL::sym_constraint.

Definition at line 101 of file path.cc.

The documentation for this class was generated from the following files:

Generated on Mon Mar 28 22:03:52 2011 for SCIL by 1.6.3