SCIL::TOUR< Graph > Class Template Reference

The symbolic constraint for undirected Hamiltonian cycles. More...

#include <tour.h>

Inheritance diagram for SCIL::TOUR< Graph >:

[legend]

Collaboration diagram for SCIL::TOUR< Graph >:

[legend]

List of all members.

Classes
class	cutset_inequality
class	degree_equality
Public Member Functions
	TOUR (Graph &G_, var_map< edge_descriptor > &X)
void	init (subproblem &S)
status	standard_separation (subproblem &S)
status	fast_separation (subproblem &S)
status	feasible (solution &S)
void	info ()

Detailed Description

template<typename Graph>
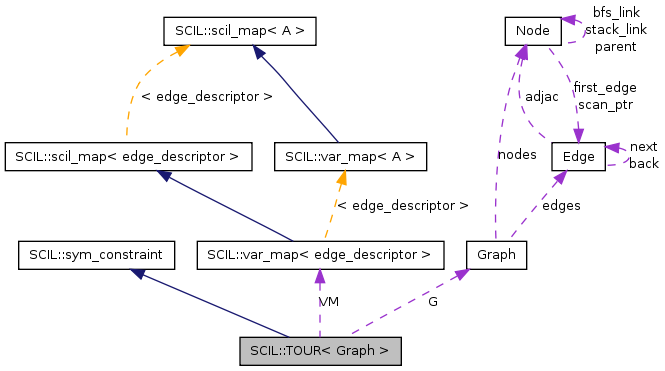
class SCIL::TOUR< Graph >

This symbolic constraints takes as arguments an undirected graph G and a var_map<edge> X. X has to map every edge of the graph to a binary variable.

The feasible assignments of the symbolic constraint are those where the vector of the variables associated with the edges of the graph is an incidence-vector of a Hamiltonian cycle.

The symbolic constraint uses the cutting plane method, based on the well known subtour elimination formulation of Hamiltonian cycles.

Definition at line 36 of file tour.h.

Constructor & Destructor Documentation

template<typename Graph >

TOUR::TOUR	(	Graph &	G_,
		var_map< edge_descriptor > &	X
	)			`[inline]`

Ensures that the edges in X form a Hamiltonian cycle.

Preconditions:

The variables associated to the edges are binary.

Parameters:

TOUR_heuristic_only true|false

For a demo, see: tsp.cc .

Definition at line 83 of file tour.cc.

Member Function Documentation

template<typename Graph >

TOUR< Graph >::status TOUR::fast_separation ( subproblem & S ) [inline, virtual]

Separates the subtour elimination constraints, i.e. 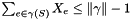$\sum_{e \in \gamma(S)} X_e \le \| \gamma \| -1$ for all 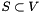$S \subset V$ , with a heuristic separation algorithm.

Reimplemented from SCIL::sym_constraint.

Definition at line 113 of file tour.cc.

References SCIL::subproblem::configuration().

template<typename Graph >

TOUR< Graph >::status TOUR::feasible ( solution & S ) [inline, virtual]

Returns true, if the induced graph is connected.

Reimplemented from SCIL::sym_constraint.

Definition at line 263 of file tour.cc.

References SCIL::subproblem::configuration(), and SCIL::solution::value().

template<typename Graph >

void TOUR::info ( ) [inline, virtual]

Returns information on the symbolic constraint.

Reimplemented from SCIL::sym_constraint.

Definition at line 292 of file tour.cc.

template<typename Graph >

void TOUR::init ( subproblem & S ) [inline, virtual]

Adds the degree constraints, i.e. 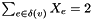$\sum_{e \in \delta(v)} X_e = 2$ for all 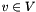$v \in V$ , to the LP.

Reimplemented from SCIL::sym_constraint.

Definition at line 95 of file tour.cc.

References SCIL::subproblem::add_basic_constraint(), and SCIL::subproblem::configuration().

template<typename Graph >

TOUR< Graph >::status TOUR::standard_separation ( subproblem & S ) [inline, virtual]

Separates the subtour elimination constraints, i.e. 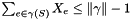$\sum_{e \in \gamma(S)} X_e \le \| \gamma \| -1$ for all 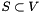$S \subset V$ , with a heuristic and an exact separation algorithm.

Reimplemented from SCIL::sym_constraint.

Definition at line 106 of file tour.cc.

References SCIL::subproblem::configuration().

The documentation for this class was generated from the following files:

SCIL::TOUR< Graph > Class Template Reference

Classes

Public Member Functions

Detailed Description

template<typename Graph> class SCIL::TOUR< Graph >

Constructor & Destructor Documentation

Member Function Documentation

template<typename Graph>
class SCIL::TOUR< Graph >